Lessons I Learned From Info About How To Tell If Two Planes Are Parallel

Find The Equation Of A Line Parallel To Plane Tessshebaylo
Unraveling Parallel Planes
1. Spotting Parallel Planes
Ever looked up at contrails in the sky and wondered if those planes were heading in the exact same direction, never to intersect? That's the essence of parallel planes. In the world of geometry, two planes are parallel if they never meet, no matter how far you extend them. Think of it like two perfectly flat sheets of paper held apart from each other. They share the same "direction" but occupy different spaces. Easy enough, right?
But how do you know for sure if they're truly parallel? This is where it gets a tad more involved, but stick with me. We need to look at something called the normal vectors of the planes. What's a normal vector, you ask? Imagine a tiny arrow sticking straight out of the plane, perpendicular to its surface. That's your normal vector!
If the normal vectors of two planes are parallel (meaning they point in the same or opposite directions), then the planes themselves are parallel. It's like checking the slopes of lines to see if they're parallel in 2D geometry, but now we're in 3D, dealing with planes and vectors. Think of it as a geometric handshake — the normal vectors need to agree!
Don't worry if the term "normal vector" sounds intimidating. We'll break it down further in the following sections, explaining how to find them and how to compare them to determine if those planes are destined to remain eternally separate. Ready to dive deeper?

Decoding the Equation
2. Extracting Normal Vectors from Plane Equations
Okay, so we know normal vectors are key to figuring out if planes are parallel. But how do we actually find them? Luckily, the equation of a plane is practically screaming the answer at us! A plane's equation is typically written in the form Ax + By + Cz + D = 0, where A, B, and C are constants, and x, y, and z are the coordinates in space. These constants are the coefficients of x, y, and z. Guess what? Those coefficients (A, B, C) form the components of the normal vector!
Thats right, the normal vector is simply (A, B, C). Seriously, that's it! It's like finding a hidden treasure right in plain sight. Let's say we have a plane with the equation 2x + 3y - z + 5 = 0. The normal vector for this plane would be (2, 3, -1). Notice how the -1 comes from the -z term.
So, whenever you see an equation of a plane, just pluck out those coefficients, and you've got your normal vector. The number D in the equation (the constant term) doesn't affect the direction of the plane, so we can ignore it when determining if planes are parallel. D only shifts the plane's position in space.
Now, let's consider another plane equation: -4x - 6y + 2z - 10 = 0. The normal vector here is (-4, -6, 2). Do these vectors look related? We'll explore that in the next section when we talk about parallel vectors! Getting the hang of this, I hope?

Parallel Planes
Vector Vibes
3. Determining Parallel Vectors
We've got our normal vectors; now comes the crucial step: determining if they're parallel. Remember, two vectors are parallel if one is a scalar multiple of the other. This means you can multiply one vector by a single number (a scalar) to get the other vector.
Let's revisit our example from the previous section. Plane 1 has a normal vector of (2, 3, -1), and Plane 2 has a normal vector of (-4, -6, 2). Can we multiply (2, 3, -1) by some number to get (-4, -6, 2)? The answer is yes! If we multiply (2, 3, -1) by -2, we get exactly (-4, -6, 2).
Since one normal vector is a scalar multiple of the other, we can confidently say that the normal vectors are parallel. This means, drumroll pleasethe planes are parallel! Woo-hoo! But what if it's not so obvious? Sometimes the numbers aren't as neat and tidy. What if we had vectors (1, 2, 3) and (2, 4, 5)? In that case, they aren't parallel, because you can't multiply (1, 2, 3) by one number to get (2, 4, 5). If they're not scalar multiples, then the planes aren't parallel.
Keep in mind that the scalar multiplier can be positive or negative. A negative multiplier means the vectors are pointing in opposite directions, but they're still considered parallel for the purpose of determining if the planes are parallel. Think of it as two cars driving in opposite directions on the same straight road — they're still going in the same direction even though they're heading away from each other!

Beyond Parallel
4. Understanding Intersecting and Coincident Planes
So, what happens if the normal vectors aren't parallel? Well, that means the planes aren't parallel either. They're either intersecting or coincident. Intersecting planes are like the pages of an open book — they meet along a line. The angle between the planes is determined by the angle between their normal vectors.
Coincident planes, on the other hand, are the exact same plane, just described with potentially different equations. They completely overlap each other. Think of it as two sheets of paper perfectly stacked on top of one another.
To determine if non-parallel planes intersect or are coincident, youd need to solve the system of equations representing the planes. If there's a solution, they intersect. If there's an infinite number of solutions and the planes' equations are scalar multiples of each other (including the constant term), then they're coincident. This requires more in-depth linear algebra, but just knowing the basics gives you a good start.
Understanding these distinctions is crucial in various fields, from computer graphics (where accurately representing intersections is vital) to engineering (where spatial relationships affect design). So even though we're focusing on parallel planes here, knowing the alternatives is a good brain exercise!

Copyright © Cengage Learning. All Rights Reserved. Ppt Download
Real-World Relevance and Applications
5. Why This Matters in the Real World
You might be thinking, "Okay, I can tell if two planes are parallel. So what? When will I ever use this in real life?" Well, believe it or not, this concept pops up in more places than you might think. Let's start with computer graphics. When designing 3D models or creating virtual environments, understanding the relationships between planes is crucial for rendering realistic scenes. Are the walls of a room parallel? Are the panels of a spaceship aligned correctly? The answer depends on this knowledge.
Then there's architecture and construction. Ensuring that walls, floors, and ceilings are parallel or perpendicular is fundamental for structural integrity and aesthetic appeal. Imagine a building with floors that aren't parallel — it would be a nightmare to furnish and incredibly unstable! Precise angle calculations are essential to prevent structural problems and costly mistakes, and, this skill will ensure that the rooms of a building are livable.
Beyond those specific applications, the ability to visualize and reason about spatial relationships is generally valuable. It helps with problem-solving in various fields and allows you to understand the world around you with greater depth. It's like having a secret geometric superpower!
So, the next time you're admiring a well-designed building or marveling at a realistic computer-generated image, remember that the principles of parallel planes (and their intersections) played a role in making it all possible. Geometry is all around us, shaping the world we inhabit. And sometimes, understanding even a seemingly simple concept like parallel planes can open up a whole new perspective.
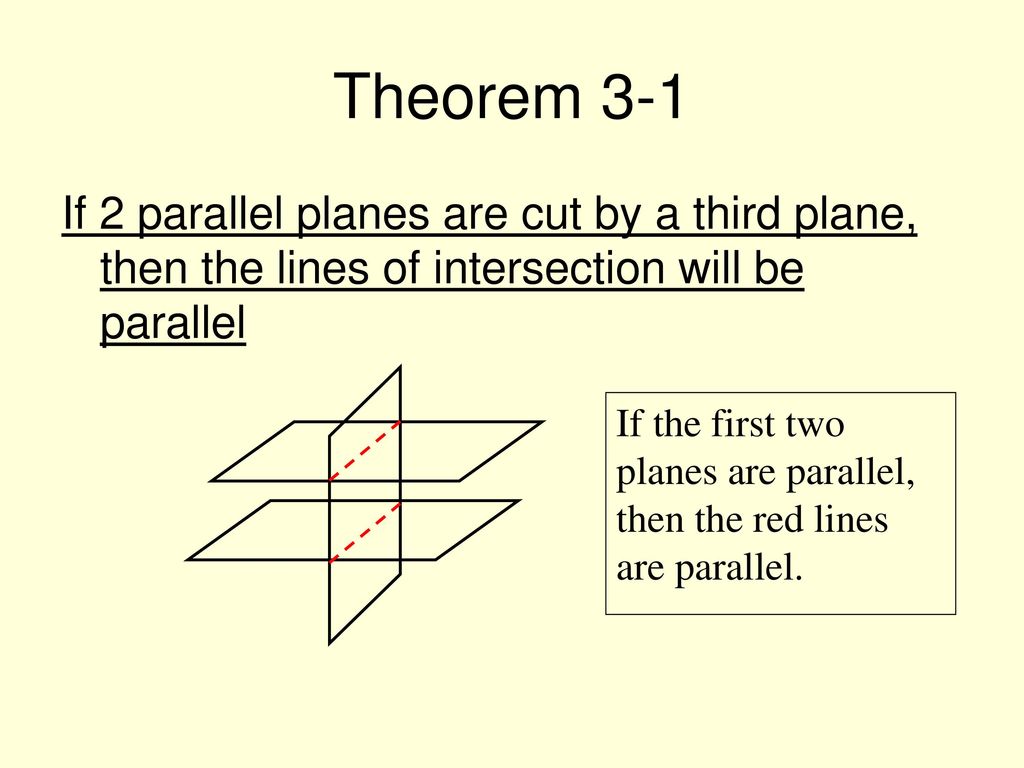
2 Parallel Planes
FAQ
6. Frequently Asked Questions
Q: What happens if the normal vectors are perpendicular (dot product equals zero)?A: If the normal vectors are perpendicular, the planes themselves are also perpendicular. This means they intersect at a right angle.
Q: Does the value of 'D' in the plane equation (Ax + By + Cz + D = 0) affect whether the planes are parallel?A: No, the value of 'D' only affects the position of the plane in space, not its direction. Therefore, it does not affect whether two planes are parallel.
Q: Is there an easier way to check for parallel planes than finding normal vectors?A: Not really, the normal vector method is the most straightforward and reliable way to determine if two planes are parallel. While you could try to manipulate the equations directly, that can become complicated and error-prone.
Q: Can I use this method to determine if a line is parallel to a plane?A: Yes, but with a slight modification. A line is parallel to a plane if the direction vector of the line is perpendicular to the normal vector of the plane. In other words, their dot product should be zero.