One Of The Best Info About Is The Voltage Same In A Series Circuit

Unraveling the Mystery

1. Sharing the Electrical Load

Ever wondered what happens to voltage when it travels through a series circuit? It's a common question, and the answer, while not exactly rocket science, can sometimes feel a little confusing. So, let's break it down. Imagine a group of hikers climbing a mountain. The mountain is the total resistance of the circuit, and each hiker represents a resistor. The effort (voltage) required to reach the top is distributed among the hikers. Some parts of the climb might be steeper, requiring more effort from certain hikers, while other parts are easier.

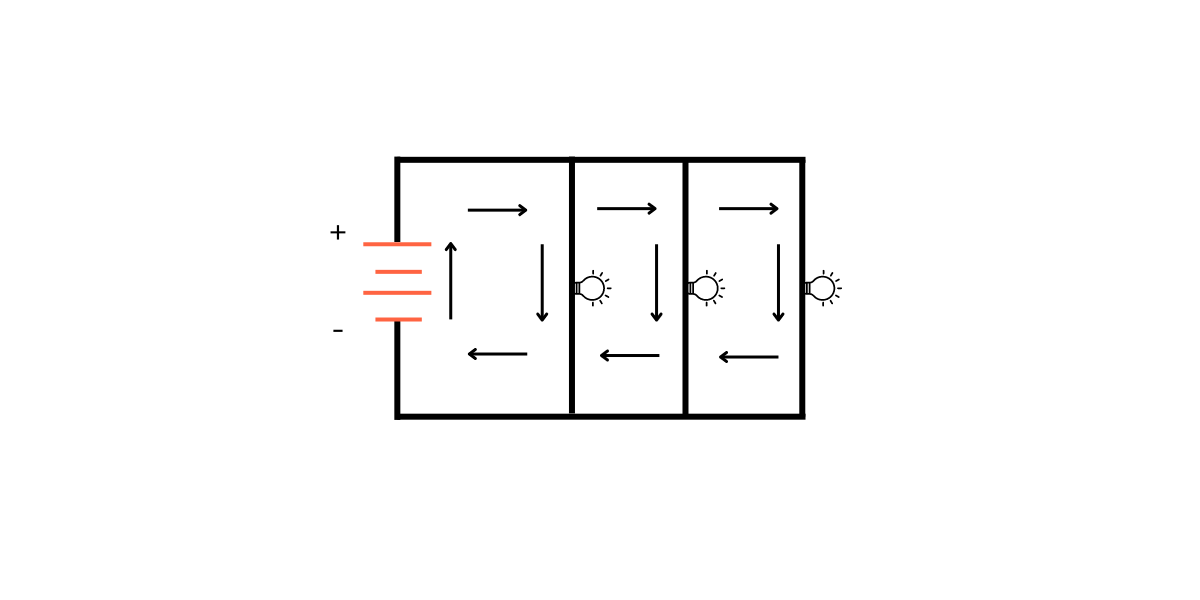
In a series circuit, components (like resistors) are connected one after the other, forming a single pathway for the electric current to flow. Think of it like that single hiking trail. The current, which is the flow of electrons, has no other route to take. Because of this single path, the current is the same throughout the entire series circuit. However, the voltage? Ah, that's where things get interesting. The voltage, which is the electrical potential difference, or the "push" behind the current, is divided among the components.

So, the straightforward answer to "Is the voltage the same in a series circuit?" is a resounding "No!" It's not the same. Each resistor "drops" some of the voltage as the current passes through it. The amount of voltage dropped depends on the resistance of each component. A higher resistance means a larger voltage drop, and vice versa. It is all about how difficult each hiker makes the climb. A big boulder will take a lot more effort to get past than a bit of gravel. So larger resistance = more voltage drop.

Here's the key takeaway: the total voltage supplied to a series circuit is equal to the sum of the individual voltage drops across each component. It's like saying the total height of the mountain is equal to the sum of all the smaller climbs each hiker must perform. This relationship is described by Kirchhoff's Voltage Law, a fundamental principle in circuit analysis. Remember, Voltage is potential difference and it doesn't remain same in series circuits. You are basically distributing it depending on the resistance.

Voltage Drop Explained

2. Understanding the Division

Let's dive a bit deeper into why the voltage drops occur. Think of it like this: each resistor in the circuit acts as a barrier to the flow of current. As the current struggles to push through the resistor, it loses some of its "oomph," which translates to a drop in voltage. The higher the resistance, the harder the struggle, and the larger the voltage drop. It really is like our hikers and those boulders!

Now, imagine you have two resistors in a series circuit. One has a resistance of 10 ohms, and the other has a resistance of 20 ohms. The 20-ohm resistor will cause a larger voltage drop because it presents a greater obstacle to the current flow. It's like one hiker suddenly coming across a tall boulder.

The proportion of voltage dropped across each resistor is directly proportional to its resistance. So, in our example, the 20-ohm resistor will drop twice the voltage of the 10-ohm resistor. This principle is used in voltage divider circuits, which are designed to provide specific voltage levels from a higher voltage source. It is a simple way to get a voltage lower than the one you are starting with.

To sum it up, the voltage isn't magically disappearing; it's being used to push the current through the resistors. And the amount used is directly related to the resistance of each component. You can calculate the voltage drop across each resistor using Ohm's Law (V = IR), where V is the voltage drop, I is the current, and R is the resistance. Get to calculating!

Kirchhoff's Voltage Law

3. The Law That Governs Series Circuits

We mentioned Kirchhoff's Voltage Law (KVL) earlier, but it's so important, it deserves its own spotlight. KVL is a fundamental law in electrical circuit theory that states that the sum of all the voltage drops in a closed loop (like a series circuit) must equal the total voltage supplied by the source. It's a simple yet powerful concept that helps us understand and analyze circuits.

In other words, what goes in must come out. The total voltage supplied by the battery or power source is distributed among the components in the circuit. No voltage is lost or gained along the way; it's simply divided up based on the resistance of each component. Imagine all the money that comes into your house must be divided among the bills, food, entertainment and hopefully a savings account. The money isn't lost, just spent.

Mathematically, KVL can be expressed as: V_source = V₁ + V₂ + V₃ + ... + V_n, where V_source is the voltage of the source, and V₁, V₂, V₃, ..., V_n are the voltage drops across each component in the series circuit. Think of this as the accounting principle for your electrical circuits. What is put in, must equal what is going out.

Using KVL, you can easily calculate the voltage drop across any component in a series circuit if you know the voltage of the source and the voltage drops across the other components. It's a handy tool for troubleshooting and analyzing circuits. It can also assist you in determining if your circuit is properly designed, which in turn assists with safety and functionality.

Putting It All Together

4. A Practical Illustration

Let's solidify our understanding with a practical example. Suppose we have a series circuit with a 12-volt battery and three resistors: R1 = 2 ohms, R2 = 4 ohms, and R3 = 6 ohms. What are the voltage drops across each resistor?

First, we need to calculate the total resistance of the circuit. Since it's a series circuit, the total resistance is simply the sum of the individual resistances: R_total = R1 + R2 + R3 = 2 + 4 + 6 = 12 ohms. It is just like summing the heights of all three boulders in our hiking analogy.

Next, we can use Ohm's Law to calculate the current flowing through the circuit: I = V_source / R_total = 12 volts / 12 ohms = 1 amp. This is the same for each part of the circuit. The pace of our hiker is the same on all parts of the trail.

Finally, we can calculate the voltage drop across each resistor using Ohm's Law again: V1 = I R1 = 1 amp 2 ohms = 2 volts; V2 = I R2 = 1 amp 4 ohms = 4 volts; V3 = I R3 = 1 amp 6 ohms = 6 volts. Notice that the sum of the voltage drops (2 + 4 + 6 = 12 volts) is equal to the voltage of the source, which confirms Kirchhoff's Voltage Law. In this case, all the money put into the system (12V) is the same amount as the voltage drop.

Series vs. Parallel

5. Highlighting the Differences

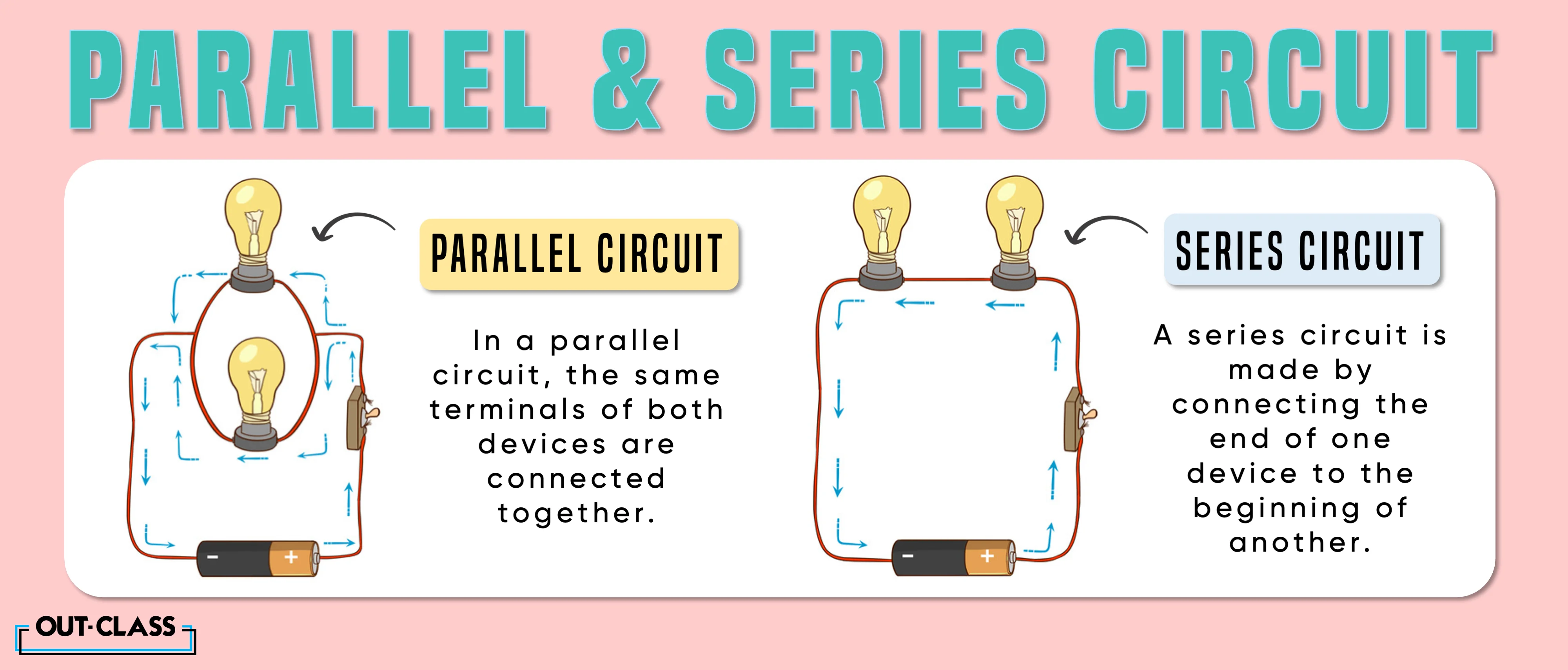
Now that we've covered series circuits in detail, let's briefly compare them to parallel circuits. This comparison will help to further clarify the concept of voltage in series circuits. In a series circuit, as we've established, the voltage is divided among the components, and the current is the same throughout the circuit. It's a single path for the current.

In contrast, in a parallel circuit, the voltage is the same across all components, and the current is divided among the branches. This means that each component receives the full voltage of the source, but the amount of current flowing through each branch depends on the resistance of that branch. So, the electrical flow has a lot of different routes to take.

Think of it like this: In a series circuit, the components are like links in a chain. If one link breaks, the entire chain is broken. But in a parallel circuit, the components are like multiple paths leading to the same destination. If one path is blocked, the other paths remain open. In the series, the hiker only has one path. In the parallel circuit, the hiker has multiple paths and is therefore able to keep going even if one path is blocked.

Understanding the difference between series and parallel circuits is crucial for designing and troubleshooting electrical systems. Knowing how voltage and current behave in each type of circuit will allow you to choose the right circuit configuration for your specific application. Depending on the design of your electrical system, you should carefully consider the use of series or parallel.

FAQ

6. Answers to Your Burning Questions

Still have questions about voltage in series circuits? Here are some common questions and their answers.

7. Q

A: If one resistor burns out in a series circuit, it creates an open circuit. This means the circuit is no longer complete, and no current can flow through it. All the other components will also stop working. Remember, it is like the hiker only has one path to travel.

8. Q

A: No. Adding more resistors will increase the total resistance of the circuit and decrease the current flow. The voltage is divided among all the resistors, so adding more resistors will simply mean each resistor gets a smaller share of the voltage. Remember, increasing the total resistance means decreasing the current.

9. Q

A: Yes, but only if all the components have zero resistance, which is practically impossible. In a real-world scenario, every component has some resistance, and therefore will cause a voltage drop. It is difficult to think of a case where each of the components has absolutely zero resistance.